アルゴリズムとアルゴリズムの評価について（高校情報I）

こんにちは！タイムレスエデュケーションの鈴木です。毎月「高校情報Ⅰ」に沿って記事を投稿しておりますが、先月は「コンピュータにおける計算」として2進法での計算方法について紹介させていただきました。本日は「アルゴリズム」について紹介させて頂きます。プログラムを作る上で必要な処理手順のことを示しますが、小学生が学習しているScratchなどでも関連があります。初学者にも分かりやすく説明させていただきますので、ぜひご覧ください。

アルゴリズム

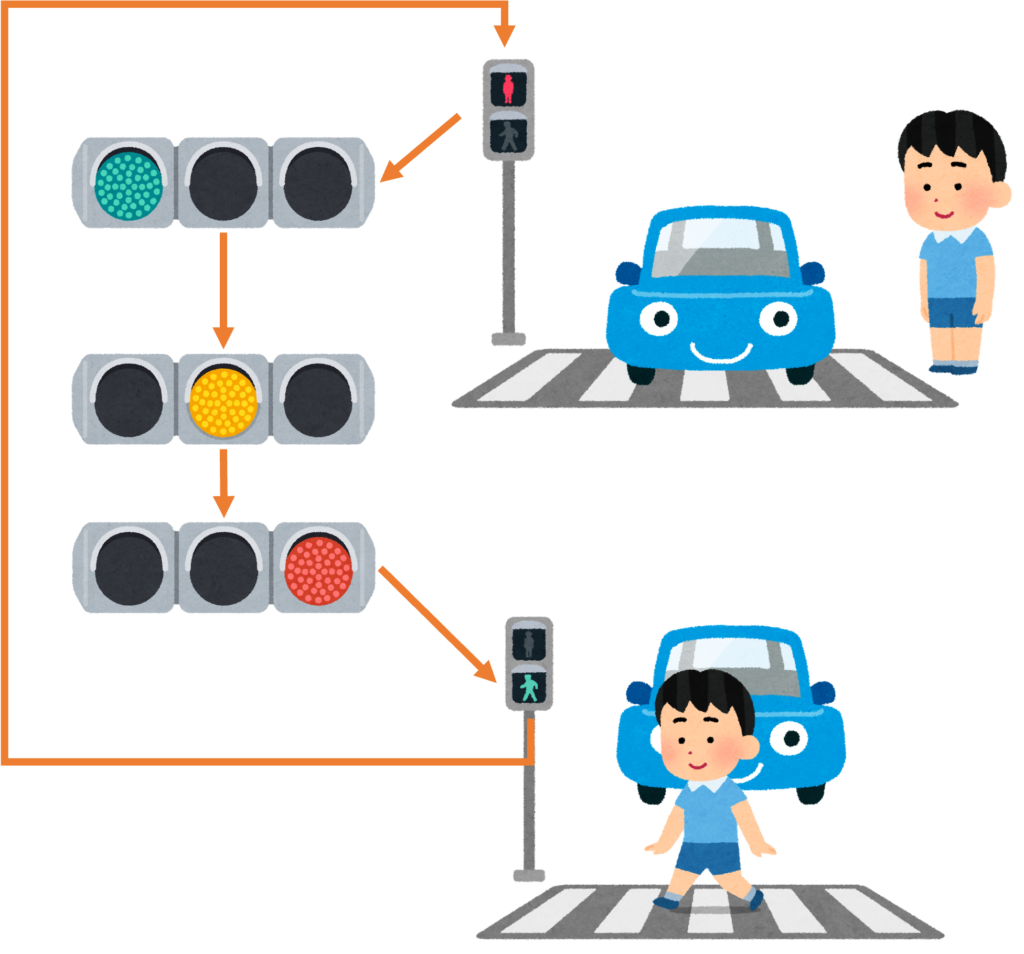
まずアルゴリズムについて、上記図のように歩行者信号と車道の信号を例に考えてみましょう。事故を防ぐためには信号の切り替えを正しく行わないといけませんね。その場合、歩行者の信号を赤にした後、車道の信号を青に切り替えます。そして、時間が経ったら車道の信号を黄→赤と切り替え、歩行者の信号を青にします。こうすることで車と歩行者が交互に道路を渡ることができるので、事故を防ぐことができますね。このように正しいアルゴリズムを構築することが、プログラムにおいては重要になっています。

アルゴリズムの基本構造

どんなに複雑なプログラムのアルゴリズムであっても、それを紐解くと3つの基本構造の組み合わせでできています。それは「逐次処理」「分岐処理」「反復処理」の3つになります。大学入学共通テストの試作問題「情報I」の大問3の中でもこれらの基本構造を使ってプログラムが書かれています。それぞれについて簡単に説明をします。

◆逐次処理

 

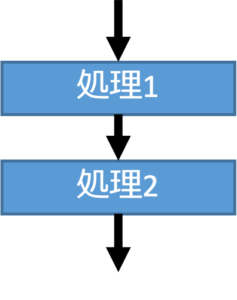
逐次という言葉は難しいですが、これは順番に処理を実行することを示します。処理1の後に処理2を行うように、順番に処理を実行することを逐次処理と言います。

◆分岐処理

 

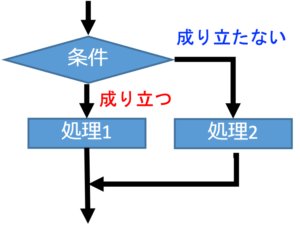
これは条件により処理を分けることを示します。図を参考に説明すると、ある条件があり、成り立つ場合は処理1を実行し、成り立たない場合は処理2を実行するように処理を切り分けることを分岐処理と言います。例えば、「車道の信号が青なら、歩道の信号は赤にする」、「スコアを10点取ったらクリアにする」など、ある条件によって処理を切り分けることができます。

◆反復処理

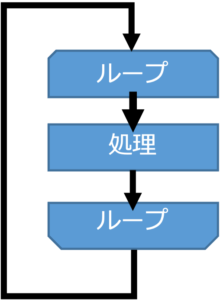
その名の通り、処理を繰り返し実行することで、ループ処理と言うことが多いです。例えば、「Aという処理を10回繰り返す」や「敵をすべて倒すまでゲームを続行する」など、ある処理をループさせることを言います。決められた回数繰り返すことや条件が成り立つまで繰り返すなど、繰り返す条件は様々あります。

アルゴリズムの効率性

正しいアルゴリズムを構築するのはもちろんですが、効率も重要になっていきます。実際の生活においても、同じ結果でもやり方によってはかかる時間が異なることがありますよね。プログラムも同様で計算量が少なくなるよう正しいアルゴリズムを構築することが重要になります。ここではあるデータを探索する場合のいくつかのアルゴリズムを例に、その計算量を比較し、効率の重要性を説明させていただきます。

<線形探索（リニアサーチ）>

線形探索（リニアサーチ）とは、あるデータ群を端から1つずつ順番に探索対象のデータであるかをチェックしていく探索方法を言います。

上記の図を参考に説明すると、探索値3を10個のデータ郡から検索するとします。人間であればひと目でどこにデータがあるか分かりますが、コンピュータにはそれができません。線形探索（リニアサーチ）の場合、端から一つずつデータを確認し、探索値3とマッチしているかを確認します。そのため、上記のデータの並びあれば、4回目に探索値とマッチし、データを見つけることができることとなります。

<二分探索（バイナリサーチ）>

二分探索（バイナリサーチ）とは、あるデータ郡の中間にある値をチェックし、探索値がそれよりも大きいか小さいかで切り分けて探索する方法です。ただし、これはデータ郡が昇順または降順にソート（並び替え）されていることが前提で使うことができるアルゴリズムとなっています。後述しますが、このソートについても代表的なアルゴリズムがあります。まずは二分探索（バイナリサーチ）について確認していきましょう。

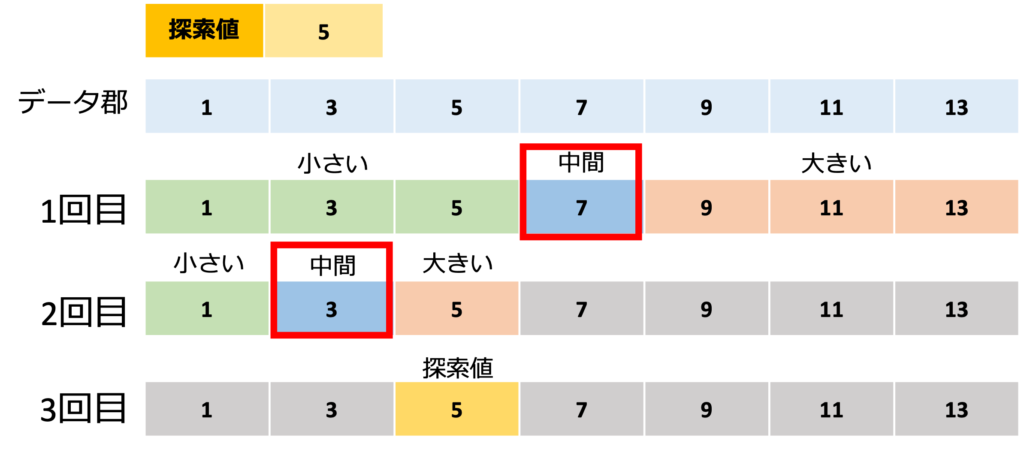
上記図を参考に説明します。まず探索値5をデータ郡から探索します。重複しますが、データ郡はソートされていることが前提で、今回は昇順にデータがソートされているものとします。そして、データ郡から中間値を選び出します。1回目の中間値は7なので探索値5は7より小さい方として切り分けられます。そして、切り分けたデータ郡からさらに中間値を選び出し、もう一度大きいか小さいかで切り分け、最終的には3回目に探索値5を見つけることができます。例えばデータの数が100個あった場合、線形探索（リニアサーチ）の場合は探索値の位置にもよりますが、最大100回データを確認する必要があることに対し、二分探索（バイナリサーチ）の場合はデータを半分、さらに半分と切り分けて探していくため、約6回でデータを見つけることができます。これを式にするとlog2nと表します。（※logは対数、2は底数、nはデータの個数）

<ハッシュ探索>

ハッシュ探索とは、ハッシュ関数と呼ばれる計算式を用いて、データの格納位置を調べて探索する方法です。もちろん、データを格納する際にはハッシュ関数を使って格納位置を決めています。

図の通り探索値をハッシュ関数を使って計算することで、格納位置が分かり、すぐにデータを見つけることができます。ただし、ハッシュ関数の計算結果が同じになる場合もあり、その場合は「オープンアドレス法」、「チェイン法」などを用いて対応します。詳しい内容は省きますが、気になる方は調べてみてください。

<アルゴリズムの評価>

ここまでデータを探索するアルゴリズムを3つ紹介させていただきました。ここからさらに重要なのが、そのアルゴリズムを評価することになります。つまり、どのアルゴリズムを選ぶことが一番効率が良いのかを考えなくてはいけません。その方法として、「オーダー記法」と呼ばれる関数の極限における値の変化を大まかに評価するための記法があります。下図に3つの探索アルゴリズムを式と図で表現していますが、対象データ数が増えた場合、計算量に違いが見えることが分かるかと思います。n個のデータから探索する場合、線形探索（リニアサーチ）は「O(n)」、二分探索（バイナリサーチ）は「O(log2n)」（※logは対数、2は底数）、ハッシュ探索は「O(1)」と表すことができます。線形探索（リニアサーチ）はデータの数だけ計算が必要になり、ハッシュ探索はデータの格納位置が分かるので計算量は一定です。二分探索（バイナリサーチ）は先程説明しましたが、データ量に対して計算量が半分、さらに半分とn÷2を繰り返していくため、データ量が増えると計算量が減っていく傾向にあります。

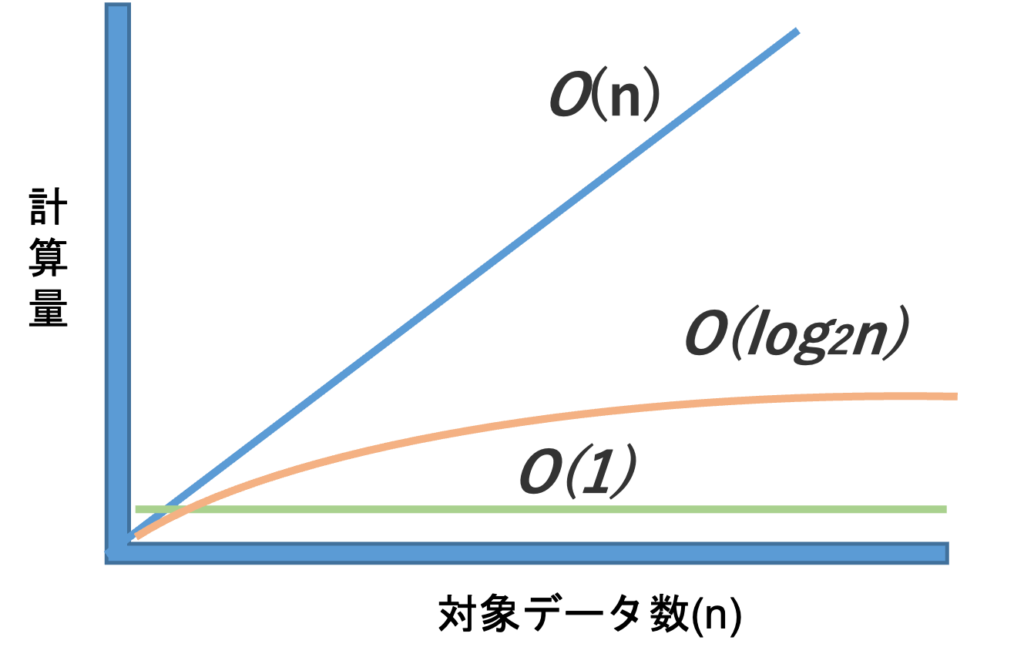
この評価だけを見ると二分探索（バイナリサーチ）かハッシュ探索を使えばいいのかと考えるかもしれません。しかし、二分探索（バイナリサーチ）の場合はデータをソートする必要があり、ハッシュ探索の場合はハッシュ関数の計算が必要なるため、一概にもそうとは言えません。システム全体を考慮して、アルゴリズムを選択する必要があります。

ソートのアルゴリズム

二分探索（バイナリサーチ）の説明の中でデータをソートするためのアルゴリズムがあることを紹介しました。代表的なものがいくつかあるですが、「バブルソート」、「クイックソート」の2つを例に紹介させていただきます。

<バブルソート>

バブルソートは、隣接する値同士の比較/入れ替えを繰り返すことで、値を昇順または降順に整列させる方法です。

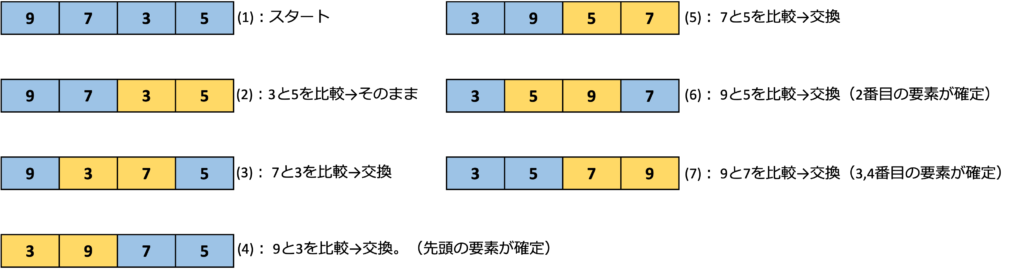
上記図を参考に説明をします。例えば「9,7,3,5」という並びのデータを昇順に並び替えようとします。まず右端二つのデータ（3と5）を比較します。今回は昇順にするので左側に小さい値、右側に大きい値としますので、ここでは並び替えはしません。そして、真ん中二つのデータ（7と3）を比較します。先程のルールでデータを並び替えたいので、7と3を交換します。そして、最後に左端二つのデータ（9と3）を比較します。ここも並び替えとしますが、この時点で先頭の要素が一番小さい値と確定しますね。このように比較と入れ替えを繰り返し、データを昇順に整列させることができます。

<クイックソート>

クイックソートは、ピボットと呼ばれる基準値を決め、データ群を基準以上と基準未満の2グループに分割し、繰り返し要素を入れ替えて整列させる方法です。

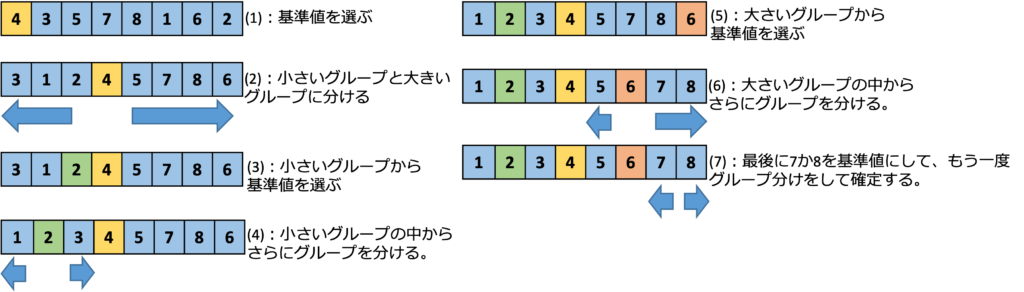
こちらも図に沿って説明します。まずピボット（基準値）を決めます。今回は中央値をピボットとし、対象の値は4となります。そして、4を基準に小さいグループと大きいグループに分けます。そしてさらに小さいグループの中からピボット（基準値）を決め、さらに小さいグループと大きいグループに分けていきます。これを繰り返すことで最終的にはデータを昇順に整列させることができます。

<その他のソートアルゴリズム>

その他には、「マージソート」、「選択ソート」、「挿入ソート」、「ヒープソート」などの代表的なソートアルゴリズムがあります。ここでは名前のみ紹介としますが、詳細が気になる方は調べてみてくださいね。

まとめ

最後までご覧いただきありがとうございました！今回は「アルゴリズム」と「アルゴリズムの効率」について紹介させていただきました。探索とソートのアルゴリズムをいくつか説明しましたが、これらのアルゴリズムも3つの基本構造で組み立てることができるとお分かり頂けたかと思います。どんなに難しい内容であっても基本構造の組み合わせだと分かると少し考えも整理できるかなと思います。高校情報Ⅰに沿って紹介しておりますが、3つの基本構造については当教室のジュニアコースの内容でも扱っています。プログラミングに興味がありましたら、ぜひお問い合わせくださませ。本日もありがとうございました。

参考文献：

黒上晴夫、堀田龍也、村井純、「情報Ⅰ」、日本文教出版株式会社、2022年1月